INTRODUCTION
It wasn't until over 100 years after Newton that the idea of energy became incorporated into Physics, but today it permeates every branch of the subject.
It's difficult to give a precise definition of energy; there are different forms of energy because there are different kinds of forces. There's gravitational energy (a meteor crashing into the Earth), elastic energy (a stretched rubber band), thermal energy (an oven), radiant energy (sunlight), electrical energy (a lamp plugged into a wall socket), nuclear energy (nuclear power plants), and mass energy (the heat of Einstein's equation E = mc2).
Energy can come into a system or leave it via various interactions that produce changes. One of the best definitions we know reads as follows: Force is the agent of change, energy is the measure of change, and work is the way of transferring energy from one system to another. And one of the most important laws in Physics (the Law of Conservation of Energy, also known as the First Law of Thermodynamics) says that if you account for all its various forms, the total amount of energy in a given process will stay constant; that is, it will be conserved. For example, electrical energy can be converted into light bulb equals the total amount of light and heat given . Energy cannot be created or destroyed; it can only be transfered (form one system to another) or transformed (from one form to another).
WORK
When you lift s book from the floor, you exert a force on it, over a distance, and when you push a crate across the floor, you also exert a force on it, over a distance. The application of force over a distance, and the resulting change in energy of the system that the force acted on, give rise to the concept of work.
When you hold a book in your hand, you exert a force on the book (normal force) but, since the book is at rest, the force does not act through a distance, so you do no work on the book. Although you did work on the book as you lifted it from the floor, once it's at rest in your hand, you are no longer doing work on it.
Definition: If a fore F acts over a distance d, and F is parallel to d, then the work done by F is the product of force and distance: W = Fd.
In Physcis, mechanical is the amount of energy transfered by a force acting through a distance. It is a scalar (a quantity that has magnitude but no direction) quantity with SI unit of joules with the symbol (J). The term work was first coined in 1826 by the French mathematician Gaspard-Gustave Coriolis.
Example:
You slowly lift a book of mass 2 kg at constant velocity a distance of 3 m. How much work did you do on the book?
Solution:
In this case, the force you exert must balance the weight of the book (otherwise the velocity of the book wouldn't be constant), so F = mg = (2 kg) (9.8 m/s2) = 20 N. Since this force is straight upward and the displacement of the book is also straight upward, F and d are parallel, so the work done by your lifting force is W = Fd = (20 N) (3 m) = 60 (N)(m). The unit for work, the newton-meter is renamed a joule and abbreviated J. So the work done here is 60J.
The definition above takes care of cases in which F is parallel to the motion. If F is not parallel to the motion, then the definition needs to be generalized.
Definition: If a force F acts over a distance d, and teta is the angle between the F and d, then the work done by F is the product of the component of force in the direction of the motion and the distance: W = ( F cos teta) d.
Example: A 15 kg crate is moved along a horizontal floor by a warehouse worker who's pulling on it with a rope that makes a 30 degrees angle with the horizontal. The tension in the rope is 200 N and the crate slides a distance of 10 m. How much work is done on the crate by the worker?
Solution: The figure below shows that F sub T and d are not parallel. It's only the component of the force acting along the direction of motion, F sub T cos teta, that does work.
Therefore,
Test Yourself
1.) In the previous example, assume that the coefficient of kinetic friction between the crate and the floor is 0.4.
a.) How much work is done by the normal force?
b.) How much work is done by the friction force?
2.) A box slides down an inclined plane (inclined plane = 40 degrees. The mass of the block, m, is 35 kg, the coefficient of kinetic friction between the box and the ramp is 0.3 and the length of the ramp d is 8 m.
a.) How much work is done by the gravity?
b.) How much work is done by the normal force?
c.) How much work is done by friction?
d.) What is the total work done?
- UNIT
The SI unit of work is the joule (J), which is defined as the work done by a force of one newtonacting over a distance of one meter. This definition is based on Sadi Carnot's 1824 definition of work as "weight lifted through a height", which is based on the fact that early steam engines were principally used to lift buckets of water, through a gravitational height, out of flooded ore mines. The dimensionally equivalent newton-meter (N·m) is sometimes used instead; however, it is also sometimes reserved for torque to distinguish its units from work or energy.
- JOULE
It is equal to the energy expended (or work done) in applying a force of one newton through a distance of one meter (1 newton meter or N·m), or in passing an electric current of one ampere through a resistance of one ohm for one second. It is named after the English physicist James Prescott Joule.
In terms of other SI units:
where N is Newton, m is meter, kg is kilogram, s is second, Pa is Pascal, and W is Watt.
One joule can also be defined as:
- The work required to move an electric charge of one coulomb through an electrical potential difference of one volt, or one '"coulomb volt" (C·V). This relationship can be used to define the volt.
- The work required to produce one watt of power for one second, or one "watt second" (W·s) (compare kilowatt hour). This relationship can be used to define the watt.
- ZERO WORK
Work can be zero even when there is a force. The centripetal force in a uniform circular motion, for example, does zero work since the kinetic energy of the moving object doesn't change. This is because the force is always perpendicular to the motion of the object; only the component of a force parallel to the velocity vector of an object can do work on that object. Likewise when a book sits on a table, the table does no work on the book despite exerting a force equivalent to mg upwards, because no energy is transferred into or out of the book.
-MATHEMATICAL CALCULATION
Force and Displacement
Force and displacement are both vector quantities and they are combined using the dot product to evaluate the mechanical work, a scalar quantity:
- W = F ·d = Fd cos
where 
is the angle between the force and the displacement vector.
is the angle between the force and the displacement vector.In order for this formula to be valid, the force and angle must remain constant. The object's path must always remain on a single, straight line, though it may change directions while moving along the line.
In situations where the force changes over time, or the path deviates from a straight line, equation is not generally applicable although it is possible to divide the motion into small steps, such that the force and motion are well approximated as being constant for each step, and then to express the overall work as the sum over these steps.
The general definition of mechanical work is given by the following line integral:
where:
is the path or curve traversed by the object;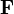
is the force vector; and
is the position
is an inexact
is path-dependent and cannot be differentiated to give 
.Equation (2) explains how a non-zero force can do zero work. The simplest case is where the force is always perpendicular to the direction of motion, making the integrand always zero. This is what happens during circular motion. However, even if the integrand sometimes takes nonzero values, it can still integrate to zero if it is sometimes negative and sometimes positive.
The possibility of a nonzero force doing zero work illustrates the difference between work and a related quantity, impulse, which is the integral of force over time. Impulse measures change in a body's momentum, a vector quantity sensitive to direction, whereas work considers only the magnitude of the velocity. For instance, as an object in uniform circular motion traverses half of a revolution, its centripetal force does no work, but it transfers a nonzero impulse.
ENERGY
Energy is a quantity that is often understood as the ability a physical system has to produce changes on another physical system.
The changes are produces when the energy is transferred from a system to another. A system can transfer energy by means of three ways, namely: physical or thermodynamical work, heat transfer, or mass transfer.
This quantity can be assigned to any physical system. The assigned energy, according to Classical Physics, depends on its physical state relative to the frame of reference used to study it.
On the other hand, in Relativistic Physics, when using an inertial reference frame, invariant mass energy is independent of such kind of reference frames. The invariant mass of a system is the same in all the inertial reference frames,it means that its energetic equivalent (invariant mass energy) would be the same in all the inertial reference frames, too.
All the forms of energy that a system has can belong to one of two great components: the internal energy and the external energy. All kinds of internal and external energies can, additionally, be classified as kinetic energy or potential energy. Kinetic Energy considers the mass and the motion of a system. If the system is studied as a whole, it is called external kinetic energy. The thermal energy is the internal kinetic energy and it considers the motion of every constitutive particle of the system. The gravitational potential energy is an external potential energy and so is the electrostatic potential energy. The elastic energy is an internal potential energy. The forms of energy are often named after a related force, as in the previous examples.
Some forms of energy are associated to the particle-like behavior of the system. But, there might be cases like that of sound energy in which the energy overall effect is related to the wave-like behavior of the system. In the specific case of sound, there is a transmission of oscillations in the pressure through the system. The energy associated to the sound wave converts back and forth between the elastic potential energy of the extra compression or lateral displacement strain of the matter and the kinetic energy of the oscillations of the medium of which the system is made up.
German physicist Hermann von Helmholtz established that all forms of energy are equivalent - energy in one form can disappear but the same amount of energy will appear in another form. A restatement of this idea is that energy is subject to a conservation law over time.
Any form of energy can be transformed into another form. When energy is in a form other than thermal energy, it may be transformed with good or even perfect efficiency, to any other type of energy, due to the second law of thermodynamics. As an example, when oil reacts with oxygen, potential energy is released, since new chemical bonds are formed in the products which are more stable than those in the oil and oxygen. The released energy resulting from this process may be converted directly to electricity with good efficiency. Alternately, it may be converted into thermal energy if the oil is simply burned. In the latter case, however, some of the thermal energy can no longer be used to perform work at that temperature, and is said to be "degraded." As such, it exists in a form unavailable for further transformation. The remainder of the thermal energy may be used to produce any other type of energy, such as electricity.
In all such energy transformation processes, the total energy remains the same. Energy may not be created nor destroyed. This principle, the conservation of energy, was first postulated in the early 19th century, and applies to any isolated system.
Although the total energy of a system does not change with time, its value may depend on the frame of reference. For example, a seated passenger in a moving airplane has zero kinetic energy relative to the airplane, but non-zero kinetic energy relative to the Earth.
- KINETIC ENERGY
The kinetic energy of an object is the energy which it possesses due to its motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes. The same amount of work is done by the body in decelerating from its current speed to a state of rest.
The speed, and thus the kinetic energy of a single object is frame-dependent (relative): it can take any non-negative value, by choosing a suitable inertial frame of reference. For example, a bullet passing an observer has kinetic energy in the reference frame of this observer, but the same bullet is stationary, and so has zero kinetic energy, from the point of view of an observer moving with the same velocity as the bullet. By contrast, the total kinetic energy of a system of objects cannot be reduced to zero by a suitable choice of the inertial reference frame, unless all the objects have the same velocity. In any other case the total kinetic energy has a non-zero minimum, as no inertial reference frame can be chosen in which all the objects are stationary. This minimum kinetic energy contributes to the system's invariant mass, which is independent of the reference frame.
In classical mechanics, the kinetic energy of a non-rotating object of mass m traveling at a speed v is mv2/2. In relativistic mechanics, this is only a good approximation when v is much less than the speed of light.
- POTENTIAL ENERGY
In Physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule (symbol J). The term "potential energy" was coined by the 19th century Scottish engineer and physicist William Rankine.
Potential energy exists when a force acts upon an object that tends to restore it to a lower energy configuration. This force is often called a restoring force. For example, when a spring is stretched to the left, it exerts a force to the right so as to return to its original, unstretched position. Similarly, when a mass is lifted up, the force of gravity will act so as to bring it back down. The action of stretching the spring or lifting the mass requires energy to perform. The energy that went into lifting up the mass is stored in its position in the gravitational field, while similarly, the energy it took to stretch the spring is stored in the metal. According to the law of conservation of energy, energy cannot be created or destroyed; hence this energy cannot disappear. Instead, it is stored as potential energy. If the spring is released or the mass is dropped, this stored energy will be converted into kinetic energy by the restoring force, which is elasticity in the case of the spring, and gravity in the case of the mass. Think of a roller coaster. When the coaster climbs a hill it has potential energy. At the very top of the hill is its maximum potential energy. When the car speeds down the hill potential energy turns into kinetic. Kinetic energy is greatest at the bottom.
The more formal definition is that potential energy is the energy difference between the energy of an object in a given position and its energy at a reference position.
There are various types of potential energy, each associated with a particular type of force. More specifically, every conservative force gives rise to potential energy. For example, the work of an elastic force is called elastic potential energy; work of the gravitational force is called gravitational potential energy; work of the Coulomb force is called electrical potential energy; work of the strong nuclear force or weak nuclear force acting on the baryon charge is called nuclear potential energy; work of intermolecular forces is called intermolecular potential energy. Chemical potential energy, such as the energy stored in fossil fuels, is the work of the Coulomb force during rearrangement of mutual positions of electrons and nuclei in atoms and molecules. Thermal energy usually has two components: the kinetic energy of random motions of particles and the potential energy of their mutual positions.
Click here to view videos about potential energy:
- CONSERVATION OF ENERGY
Energy is subject to the law of conservation of energy. According to this law, energy can neither be created (produced) nor destroyed by itself. It can only be transformed.
Most kinds of energy are also subject to strict local conservation laws, as well. In this case, energy can only be exchanged between adjacent regions of space, and all observers agree as to the volumetric density of energy in any given space. There is also a global law of conservation of energy, stating that the total energy of the universe cannot change; this is a corollary of the local law, but not vice versa. Conservation of energy is the mathematical consequence of translational symmetry of time.
According to energy conservation law the total inflow of energy into a system must equal the total outflow of energy from the system, plus the change in the energy contained within the system.
This law is a fundamental principle of physics. It follows from the translational symmetry of time, a property of most phenomena below the cosmic scale that makes them independent of their locations on the time coordinate. Put differently, yesterday, today, and tomorrow are physically indistinguishable.
This is because energy is the quantity which is canonical conjugate to time. This mathematical entanglement of energy and time also results in the uncertainty principle - it is impossible to define the exact amount of energy during any definite time interval. The uncertainty principle should not be confused with energy conservation - rather it provides mathematical limits to which energy can in principle be defined and measured.
Click here to view videos about Conservation of energy:
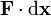Walang komento:
Mag-post ng isang Komento